Pollutant Deposition |
|||
 Previous |
 Next |
|
|
The deposition (D) from a particle is expressed
as a fraction of the mass (m) computed as the sum of different
time constants,
Dwet+dry = m {1-exp[Δt(βdry+
βgas+βinc+βbel ) ] }.
| Configure the model to run for 24 hours
with default values, from the previous Florida location of 28.5N,
80.7W using NAM 12 km data, releasing one unit over one hour. Set the
concentration grid for 0.05 degrees resolution with one output level at
zero meters (for deposition). This simulation will yield no results
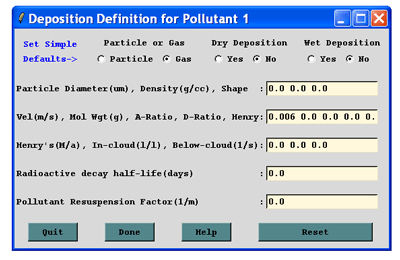
because deposition has not been activated. Open up the Deposition Setup menu
from the Concentration Setup menu and set the deposition velocity
to 0.006 m/s and leave everthing else as default. When the deposition
is entered directly as a velocity (Vd), then βdry = Vd ΔZp-1. |
 Deposition Velocity |
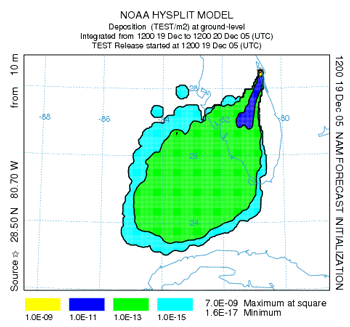
The results (below left) show the deposition left by the puff as it moved across the domain.
The dry deposition of particles due to gravitational
settling can also be computed from the particle diameter and density:
Vg = dp2 g(ρg - ρ)
(18 µ)-1.
Enter a density of 5 g/cc and a diameter of 6 um, which should result
in a settling velocity close to previous 0.6 cm/s. The results (below right)
from this configuration are almost identical
to the previous calculation.

Deposition Velocity |
 Settling Velocity |
The default approach is for the number of particles and puffs to remain the same but lose mass due to deposition. If the Deposition Probability converstion module is selected in the Advanced / Concentration Setup menu, then particles will be lost if R < βdryΔt, and where R is a random number between 0 and 1. The model must be configured for 3D particles to use this option. If a sufficient number of particles are released the results will be identical to the other deposition options. In this case, more than 15,000 particles are needed to produce a similar deposition pattern.
 |
 |